corresponde ao menor número inteiro positivo, diferente de zero, que é múltiplo ao mesmo tempo de dois ou mais números.

  é o menor número inteiro positivo que é múltiplo de todos eles simultaneamente

Propriedades do MMC

• Entre dois números primos, o MMC será o produto entre eles.
• Entre dois números em que o maior é divisível pelo menor, o MMC será o maior deles.
• Ao multiplicar ou dividir dois números por um outro diferente de zero, o MMC aparece multiplicado ou dividido por esse outro.
• Ao dividir o MMC de dois números pelo máximo divisor comum (MDC) entre eles, o resultado obtido é igual ao produto de dois números primos entre si.
• Ao multiplicar o MMC de dois números pelo máximo divisor comum (MDC) entre eles, o resultado obtido é o produto desses números.

Existem dois métodos principais para calcular o MMC: 

1. Método da lista de múltiplos:
   • Escreva os múltiplos de cada número envolvido.
2. Procure o menor número que apareça em todas as listas.
3. Exemplo: MMC de 4 e 6 
4. • Múltiplos de 4: 4, 8, 12, 16, 20, 24...
5. Múltiplos de 6: 6, 12, 18, 24...
6. O menor múltiplo comum é 12.

7. Calcular o mínimo múltiplo comum para os números 4, 6 e 12.

   • 4 = 2², 2 é um número primo;
   • 6 = 2 x 3, três também é primo;
   • 12 = 2² x 3.

   Agora pegamos os fatores primos comuns e não comuns com os maiores expoentes. Nesse exemplo temos 2 e 3 apenas. Pegamos o 2² e 3, aqui 3 está elevado ao expoente 1.

   Assim, o MMC de 4, 6 e 12 é o produto entre 2² x 3 = 4 x 3.

   Logo: MMC(4; 6; 12) = 12.

   Veja outro exemplo para clarear.

   Calcular o MMC de 80, 20, 25:

   • 80 = 2 x 2 x 2 x 2 x 5 = 2⁴ x 5;
   • 20 = 2 x 2 x 5 = 2² x 5;
   • 25 = 5 x 5 = 5².

   Dividimos 80 pelo menor número primo que neste caso foi o 2, continuamos dividindo o resultado da divisão por 2, e por último por 5 que era o menor número primos que poderíamos continuar dividindo.

   Agora peguemos os fatores primos com os maiores expoentes: 2⁴ e 5². Fazemos o produto entre eles: 2⁴ x 5² = 16 x 25 = 400.

   Daí, o MMC(80; 20; 25) = 400.

8. A decomposição simultânea ou fatoração simultânea consiste em dividir sucessivamente os números dados pelo menor fator primo, caso o número não seja divisível por aquele fator primo ele deve ser repetido.

   O MMC é obtido pela multiplicação dos fatores primos usados durante a decomposição. Veja um exemplo para você entender melhor.

   Veja como encontrar o menor múltiplo comum entre três números. Se tivermos três números 4, 6 e 8. Qual o MMC desses números através da decomposição simultânea?

   

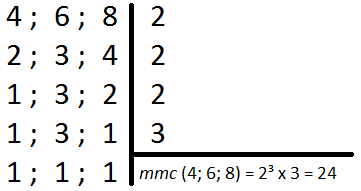
   Dividimos 4, 6 e 8 pelo menor número primo que fosse divisível por pelo menor um deles, o número 2. Depois verificamos se ainda tem números que podem ser dividido por 2, 2 e 4 são divisíveis por 2, e conservamos o 3.

   No terceiro passo, ainda é possível dividir por 2, mantemos 1 e 3. No quarto passo, só é possível dividir por 3, conservando o resto dos outros números. Quando os restos forem 1, acaba o processo.

   O MMC é a multiplicação dos números que dividimos. Utilizamos o 2 três vezes, e o 3 uma vez no processo. Assim temos: 2 x 2 x 2 ou 2³ e 3¹. Logo, 2³ x 3¹ = 24.

   Portanto, MMC(4; 6; 8) = 24

   Vamos calcular o MMC para o exemplo que usamos fatores primos, agora usando a decomposição simultânea.

   Exemplo: Calcular o MMC para 80, 20 e 25.

a) 54
b) 56
c) 58
d) 60
e) 62

2. (Vunesp) Para dividir os números 36 e 54 por respectivos menores números inteiros consecutivos de modo que se obtenham os mesmos quocientes em divisões exatas, esses números só podem ser, respectivamente:

a) 6 e 7
b) 5 e 6
c) 4 e 5
d) 3 e 4
e) 2 e 3

 (Fuvest/SP) No alto da torre de uma emissora de televisão, duas luzes “piscam” com frequências diferentes. A primeira “pisca” 15 vezes por minuto e a segunda “pisca” 10 vezes por minuto. Se num certo instante, as luzes piscam simultaneamente, após quantos segundos elas voltarão a “piscar simultaneamente”?

a) 12
b) 10
c) 20
d) 15
e) 30