Estuda a coleção de elementos.

os elementos (que podem ser qualquer coisa: números, pessoas, frutas) são indicados por letra minúscula e definidos como um dos componentes do conjunto.

Enquanto os elementos do conjunto são indicados por letra minúscula, os conjuntos, são representados por letras maiúsculas e, normalmente, com chaves { }.

Além disso, os elementos são separados por vírgula ou ponto e vírgula, por exemplo:

A = {a, e, i, o, u}

Diagrama de Euler-Venn

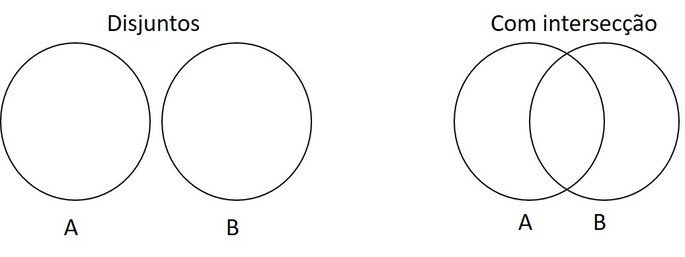
No modelo de Diagrama de Euler-Venn (Diagrama de Venn), os conjuntos são representados graficamente. Imagens como círculos, elipses e retângulos formam uma área que “guarda” seus elementos.

Esta figura plana fechada é chamada de diagrama.

Os diagramas de Venn são úteis para representar conjuntos disjuntos (nenhum elemento em comum), assim como, conjuntos com elementos que se repetem.

Exemplos
A = {x / x é uma vogal} lemos: “O conjunto A é formado pelos elementos x, tal que x é uma vogal”.

B = {x  / x é múltiplo de 3} lemos: “O conjunto B é formado pelos elementos x, tal que x pertença aos números naturais e seja um múltiplo de 3.”

Relação de Pertinência

Ela indica se o elemento pertence () ou não pertence () ao determinado conjunto, por exemplo:

D = {w,x,y,z}

Logo,

(w pertence ao conjunto D)
 (j não pertence ao conjunto D)

Isso significa que a pertinência é uma relação entre elementos e conjuntos.

Relação de Inclusão

A relação de inclusão aponta se tal conjunto está contido (C), não está contido (Ȼ) ou se um conjunto contém (Ɔ), algum subconjunto.

Exemplo:

A = {a,e,i,o,u}
B = {a,e,i,o,u,m,n,o}
C = {p,q,r,s,t}

Logo,

A C B (A está contido em B, ou seja, todos os elementos de A estão em B).
C Ȼ B (C não está contido em B, pois os elementos dos conjuntos são diferentes).
B Ɔ A (B contém A, pois todos elementos de A estão em B).

Conjunto Vazio

é o conjunto em que não há elementos;

é representado por duas chaves { } ou pelo símbolo Ø.

Note que o conjunto vazio está contido (C) em todos os conjuntos.

União, Intersecção e diferença entre conjuntos

As operações entre conjuntos são fundamentais para a solução de problemas. Cada operação possui suas características e regras.

União de conjuntos

representada pela letra (U)

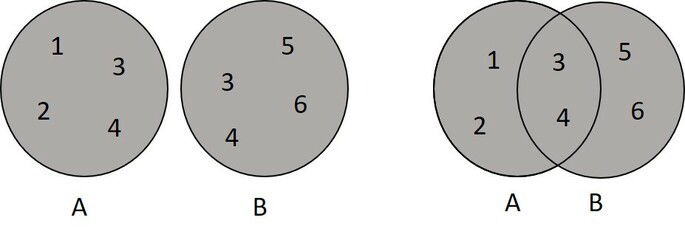
corresponde a junção dos elementos de dois ou mais conjuntos, sem repetir elementos comuns.

Exemplo

A = {1, 2, 3, 4}
B = {3, 4, 5, 6}

Logo,

A U B = {1, 2, 3, 4, 5, 6}

Repare que os algarismos 3 e 4 foram representados uma única vez, mesmo estando presentes em A e B.

Ao utilizar diagramas de Venn, a união é representada pelo preenchimento de toda imagem, não importando se são ou não disjuntos.

Intersecção de conjuntos

representada pelo símbolo (∩), corresponde aos elementos em comum de dois ou mais conjuntos.

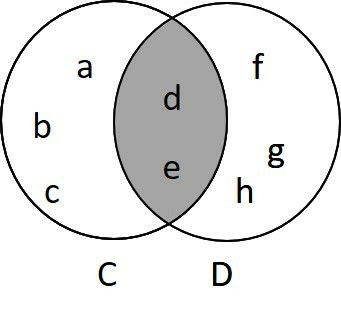
Assim, a intersecção é um novo conjunto, formado apenas pelos elementos que se repetem nos conjuntos iniciais.

Exemplo

C = {a, b, c, d, e}
D = {d, e, f, g, h}

Logo,

C ∩ D = {d, e}

Ao utilizar diagramas de Venn, a intersecção é representada pintando apenas a área onde os conjuntos estejam sobrepostos.

Essa área “guarda” apenas os elementos repetidos.

Diferença de conjuntos

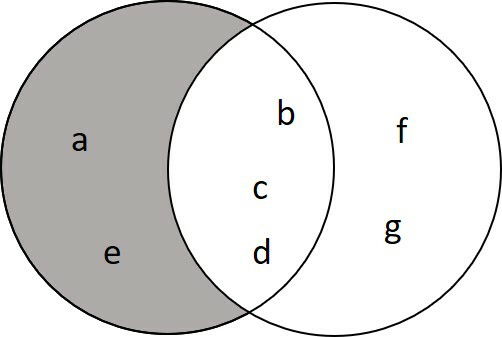
A diferença corresponde ao conjunto de elementos que estão no primeiro conjunto, e não aparecem no segundo,

Exemplo

A = {a, b, c, d, e} - B = {b, c, d, f, g}

Logo,

A - B = {a, e}

Veja que a operação retirou os elementos comuns que existem em B.

Na forma de diagrama, representamos como:

Atenção!
A subtração não é comutativa, ou seja, B - A não é igual à A - B.

B - A = {f, g}

Igualdade dos Conjuntos

Na igualdade dos conjuntos, os elementos de dois conjuntos são idênticos, por exemplo, nos conjuntos A e B:

A = {1,2,3,4,5}
B = {3,5,4,1,2}

Logo,

A = B (A igual a B).